Do I think about arithmetic wrong?

  I frequently ponder whether I think about arithmetic ‘wrong’. I don’t mean in the sense of reaching incorrect answers (although that’s sometimes the case!); I mean that the process my mind employs when attempting to solve an arithmetic problem seems rather inefficient. Let’s see if you agree!

  When you do arithmetic, what are you doing in your mind? Pay attention to what your mind is doing when you evaluate the following expressions:

• 1 + 1
• 5 + 6
• 84 - 7
• 3 x 4
• 20 x 5

  Now that you’ve had a little think about what you do in your mind, I’ll explain what I do.

  For simple calculations that I’ve memorised, the answer can just be plucked out of my mind; it just ‘comes to me’. For example when asked what 7 x 7 is, I know it’s 49, and I’ll be picturing the digits ‘49’ as I tell you that.

  However, my default method is rather different.

  I picture a number line in space, with zero just to my left, and larger numbers extending to the right, curving a little upwards. As Stanislas Dehaene explains in his book The Number Sense: How the Mind Creates Mathematics, this mental number line is consistent with that of many of us in Western society. The slight upwards curve corresponds to larger numbers being more ‘squished’ together, a bit like a logarithm. Again, this is quite typical of mental number lines (see Thinking Visually by Stephen K. Reed to read more about why).

  I then ‘find’ the answer on that line. (Yes, you read that correctly.)

  For example, for 5 + 6, I picture where 5 is on the number line, and plonk 6 on the end. By this, I mean place a bar of length 6, decomposed into 5 + 1, after 5. So 5 + 5 makes 10, and then there’s one left over that gets put above 10 in the ‘teens’ section of the number line. Ta-da, I get 11!

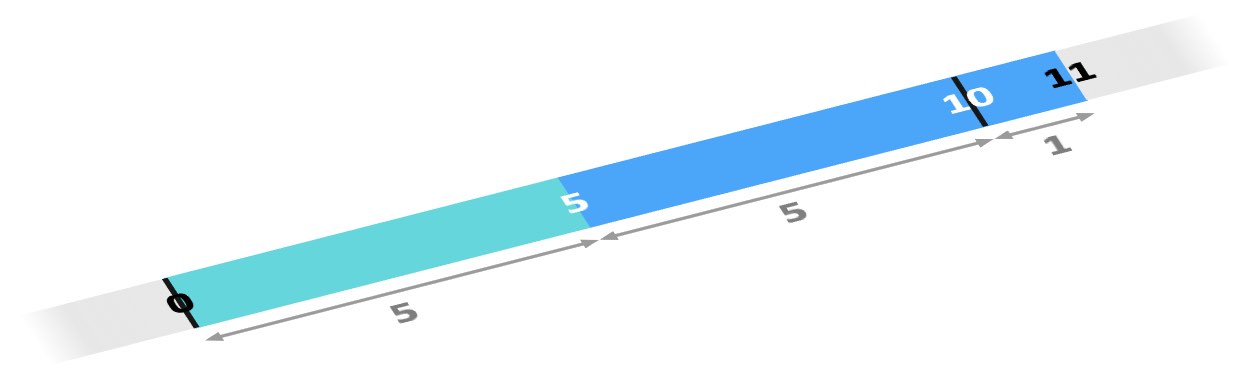
  This probably sounds overly complicated for such a simple piece of arithmetic - I agree!

  Let’s take another example: 84 - 7. I picture where 84 is on the number line, and plonk down a bar of 7 below it. This bar of 7 is made up of 4 and 3, so the 4 takes me down to 80, and the 3 down to 77. Now I know the answer: 77.

  This seems even more ridiculous now that I’ve written it out.

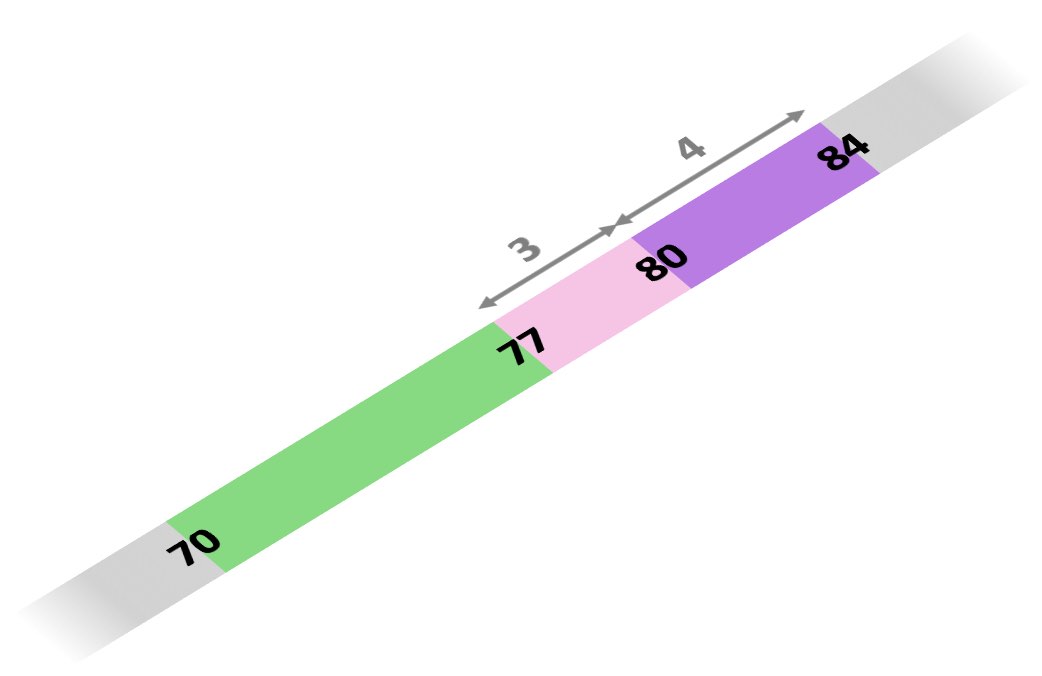
  It’s clear to me that I’m structuring my mental number line around base 10, and taking advantage of that to do arithmetic. However, forming this picture of the number line and then breaking down numbers to fit the images I’m creating seems rather convoluted; I’m actually performing far more operations in my head than I need to be doing, just so that I can use my mental image to reach the answer.

  Furthermore, my mental number line is subject to the pitfalls of associating numbers and space: I take longer to do simple arithmetic using numbers that are further apart, because I am mentally straining more to ‘see’ a greater distance. For example, 84 - 37 is slower than 44 - 37, because the distance between the numbers involved in the first subtraction is larger. Of course, I could just use that 14 - 7 = 7 before dealing with the tens digit, and not have to do this visualisation of the number line at all!

  You see what I mean by it being inefficient?

  The question gets even more interesting when we move to mental arithmetic of multiple-digit numbers. For example, what is 14 x 24? What did you do in your mind when you started calculating that?

  I didn’t even begin to calculate it: I wanted to work out the most efficient thing to be doing in my mind, so I had a little conversation with myself about what I should be doing in my mind to reach the answer! Should I picture a ‘times table grid’ that I learnt to draw out in primary school? Should I try to picture long multiplication? Do I compute a simpler multiplication and then do some addition? Should I avoid visualising anything at all? So many questions!

  It is clear to me that there is a better way of using my mind when doing arithmetic. Is there such a thing as the ‘optimal’ way, and if so, what is it?

  My question to you is this: when you do mental arithmetic, what are you doing in your mind? I’d love to hear your answers!

  Bonus thoughts to contemplate: why are we not taught what we should be doing in our minds when we perform a calculation? Is it because when we first learn arithmetic, the focus is on rote memorization rather than using our intuition and understanding of numbers? Or are we meant to do in our mind what we’d do on paper, but this parallel is never explicitly stated? Let me know your thoughts!